1.2 函数的图像
1. 基本初等函数与初等函数
基本初等函数: 常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数.
(1) 常数函数
易考 “找交点个数” 或在概率论中求概率
它为偶函数
图 1-5
(2) 幂函数
【注】(1)
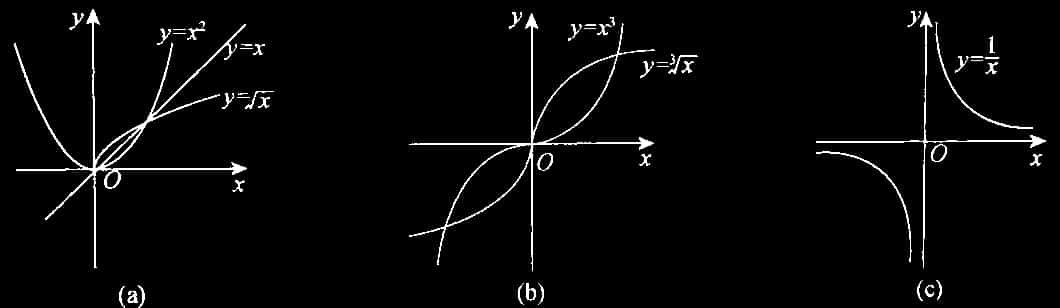
的定义域和值域取决于 的值. 当 时, 都有定义. (2) 常用的幂函数 (见图 1-6).
图 1-6
(3) 当
时,由 与 [见图 1-8(b)] 具有相同的单调性且与 具有相反的单调性, 故 ① 见到
时,可用 来研究最值; ② 见到
时,由 ,可用 来研究最值; ③ 见到
时,可用 来研究最值; ④ 见到
时,可用 来研究最值 (结论相反,即 与 的最大值点、最小值点相反). 利用以上①∼④ ,可使得计算简单方便.
【例 1.10】 设
解 取对数, 得
令
即
(3) 指数函数
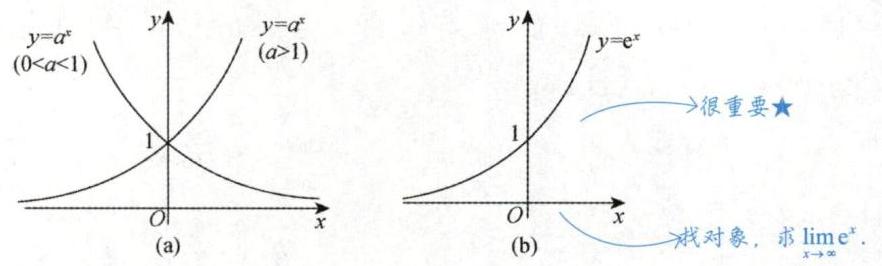
图 1-7
【注】(1) 定义域:
,值域: . (2) 单调性: 当
时, 单调增加; 当 时, 单调减少. (3) 常用的指数函数:
[见图 1-7(b)]. (4) 极限:
. (5) 特殊函数值:
. (6) 指数运算法则.
其中
是正实数, 是任意实数.
(4) 对数函数
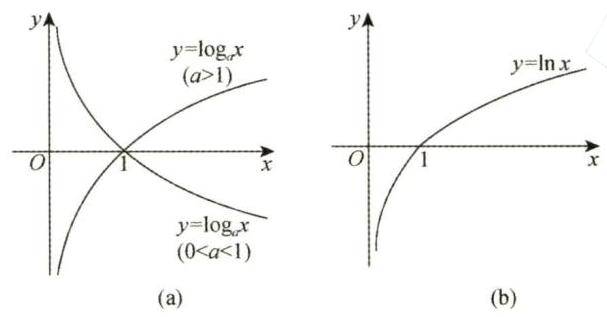
图 1-8
【注】(1) 定义域:
,值域: . (2) 单调性: 当
时, 单调增加; 当 时, 单调减少. (3) 常用的对数函数:
(自然对数: ) [见图 1-8(b)]. (4) 特殊函数值:
. (5) 极限:
. (6) 常用公式:
. (7) 对数运算法则.
①
(积的对数 对数的和). 积变和
②
(商的对数 对数的差). 商变差
③
, (幂的对数 对数的倍数). 幂次变倍数
常考: 当
时,
; ; (中值定理(拉格朗日中值定理)证明)。
【例 1.11】 已知
(A)
解 应选 (B).
由于
(5) 三角函数
一拱的面积为2.
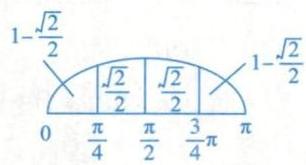
①正弦函数与余弦函数
正弦函数
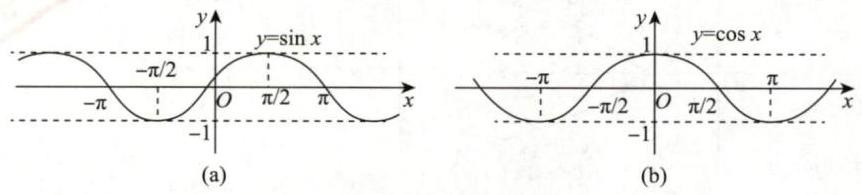
图 1-9
【注】(1) 定义域:
,值域: . (2) 奇偶性:
是奇函数, 是偶函数, . (3) 周期性:
和 均以 为最小正周期, . (4) 有界性:
. (5) 特殊函数值:
, (6)
.
②正切函数与余切函数
正切函数
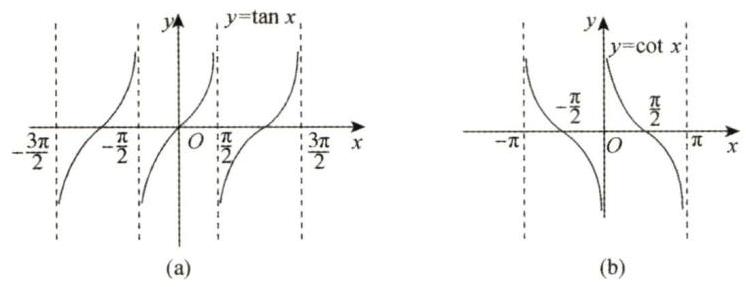
图 1-10
【注】(1) 定义域:
的定义域为 的定义域为 . 值域:
. (2) 奇偶性:
和 均为奇函数 (在其定义域内). (3) 周期性:
和 均以 为最小正周期 (在其定义域内). (4) 特殊函数值:
,
③正割函数与余割函数
正割函数
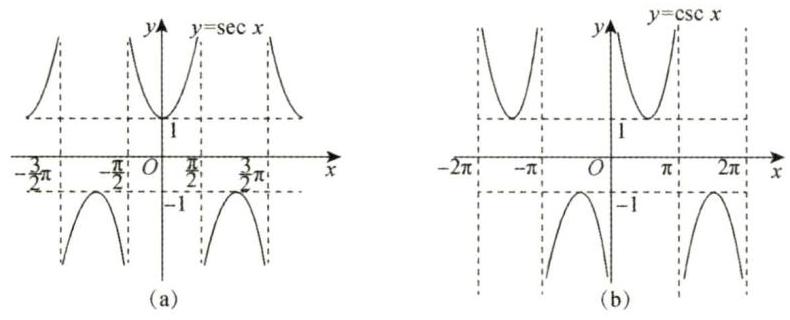
图 1-11
【注】(1) 定义域:
的定义域为 的定义域为 . 值域:
. (2) 奇偶性:
为偶函数, 为奇函数 (在其定义域内). (3) 周期性:
和 均以 为最小正周期 (在其定义域内). (4)
; .
(6) 反三角函数
①反正弦函数与反余弦函数
反正弦函数
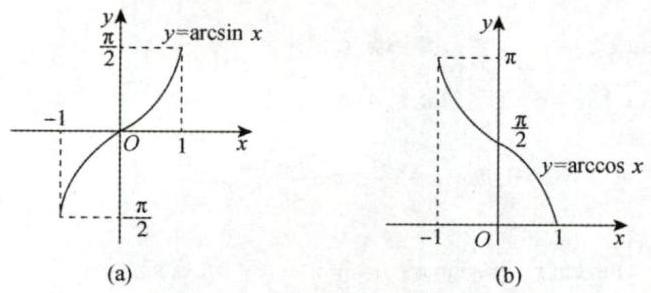
图 1-12
【注】(1) 主值区间.
的主值区间为 的主值区间为 . (2) 反三角函数的恒等式有
令
则
又
因此
即(3) 特殊函数值:
【例 1.12】 设
只有当
解 当
当
当
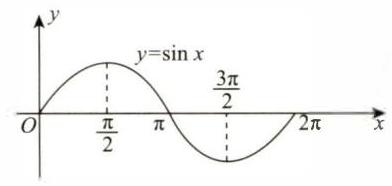
图 1-13
综上所述,
②反正切函数与反余切函数
反正切函数
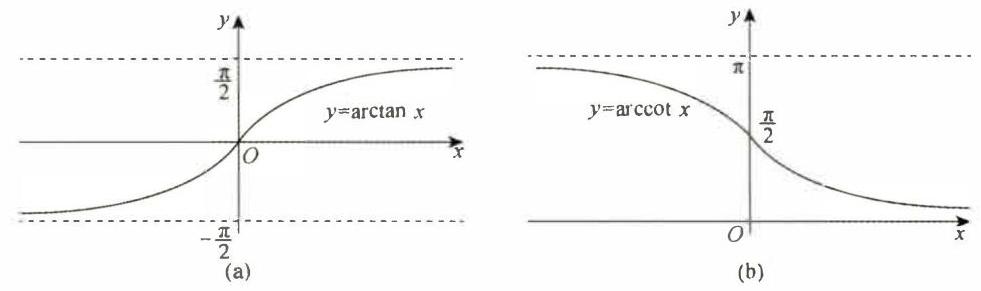
图 1-14
【注】(1) 定义域:
. 值域:
的值域为 的值域为 . (2) 单调性:
单调增加, 单调减少. (3) 奇偶性:
为奇函数 (在其定义域内). (4) 有界性: 两个函数在其定义域内有界,
. (5) 性质:
. (6) 特殊函数值:
, (7) 极限:
.
(7) 初等函数
由基本初等函数经过有限次的四则运算, 以及有限次的复合步骤所构成的并且可以由一个式子所表示的函数称为 初等函数 .
【注】(1) 初等函数的定义域可以是一个区间,也可以是几个区间的并集, 甚至可以是一些孤立的点. 例如,
的定义域是 . (2) 幂指函数
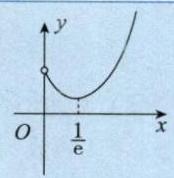
也是初等函数,如 时, 是初等函数, 其图形如图 1-15 所示. 具体作图过程见例 5.12.
图 1-15
2. 分段函数
在自变量的不同变化范围中, 对应法则用不同式子来表示的函数称为 分段函数 . 需要强调一句, 分段函数是用几个式子来表示的一个 (不是几个) 函数, 一般来说, 它不是初等函数. 分段函数的典型形式如下:
分段函数很重要, 原因在于其形式的复杂性所带来的命题的丰富性. 后面会看到, 不论是求极限、 求导数, 还是求积分, 出现最多的研究对象之一便是分段函数.
下面列出三个重要的分段函数.
①
②
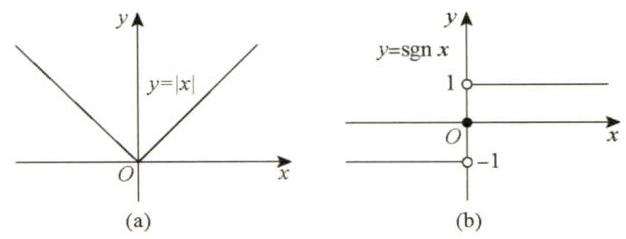
图 1-16
③
因此,取整函数
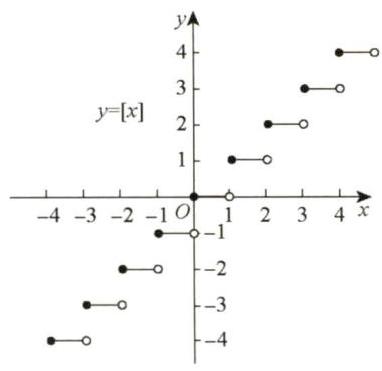
图 1-17
【注】(1)
,其中 为整数. (2)
. (3)
.
【例 1.13】 设
(A) 无界函数 (B) 单调函数
(C) 偶函数 (D) 周期函数
解 应选 (D).
由于
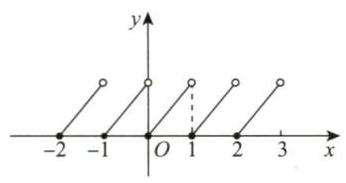
图 1-18